PROJECTS
We are interested in how complex quantum many-body systems are built up from single particles and how dimensionality and interaction strength affects the physical properties of a system. These are defining issues that arise in the description of many naturally occurring complex systems. Ultracold quantum gases allow us to create generic quantum systems with precise control over these relevant parameters: system size, interaction strength and dimensionality.
There are three experimental projects working with ultracold lithium-6 atoms. The 2D Fermion Experiment investigates correlations in systems with up to 20 particles across the BEC-BCS crossover. In the Rotating Few Fermion Experiment, a rotating trap setup is implemented to investigate Skyrmions and Quantum Hall physics. The Heidelberg Quantum Architecture setup is a next generation experiment in collaboration with Prof. Dr. Matthias Weidemüller that aims to accelerate the experimental cycle times by at least on order of magnitude.
Tools and Experimental Techniques
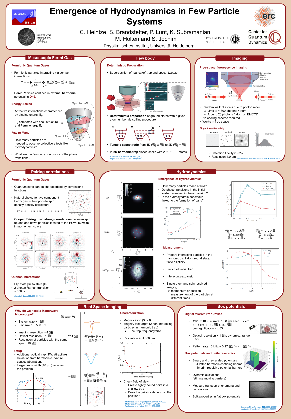
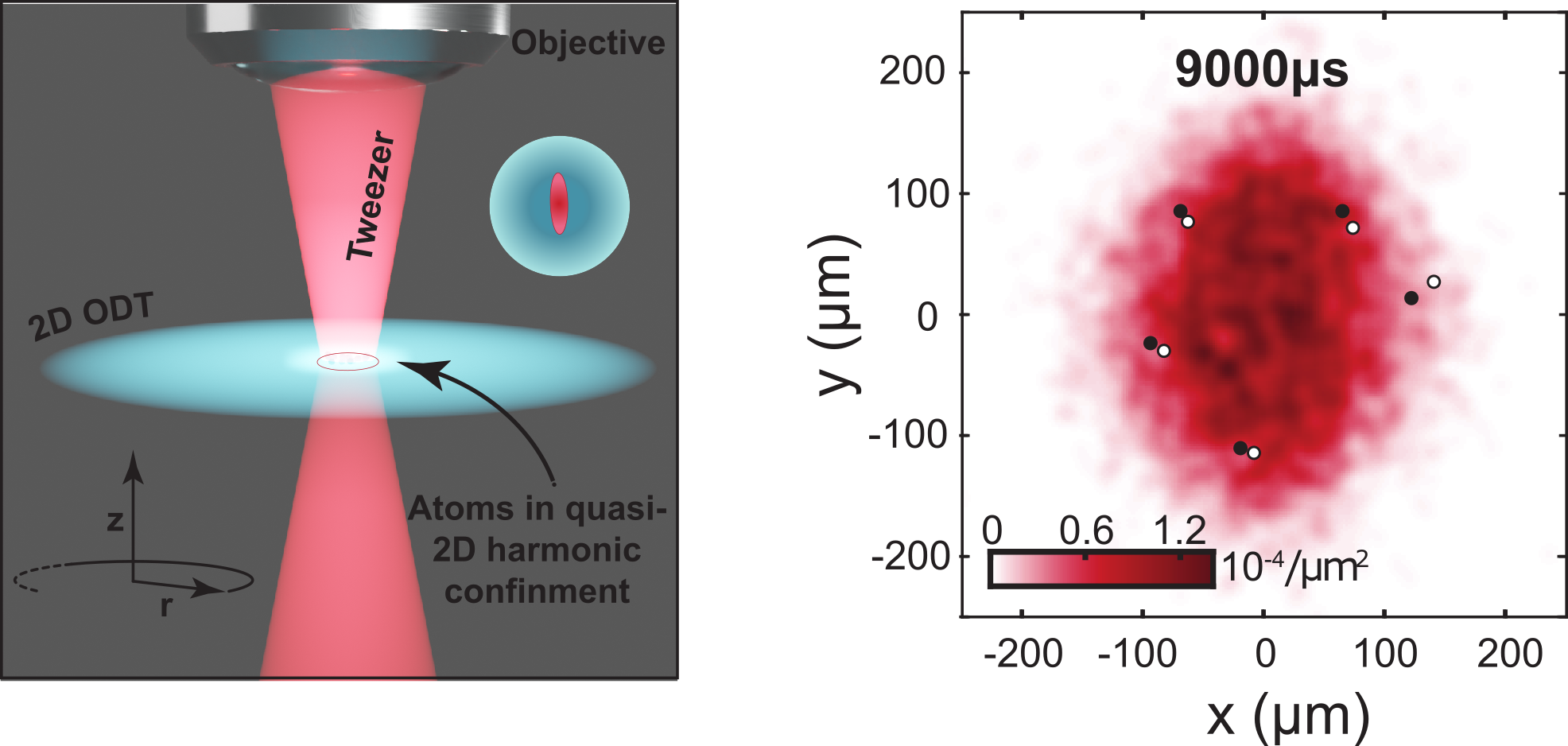
Over the years we developed several techniques which are mostly shared between our three projects. Our systems are prepared in a 2D lightsheet built up by two interfering lightbeams. To explore few particle systems on the micron scale, we shine in an optical tweezer through a high NA objective from the top. The interactions between lihtium-6 atoms in different pseudo-spin states can be controlled using a Feshbach resonance.

Deterministic preparation
We are able to prepare few fermion 1D and 2D systems deterministically. The idea is to first prepare a state of tens of fermions in a harmonic oscillator potential and let as many atoms tunnel out of the potential as the wanted number of atoms remain. For this procedure the system has to fullfil two conditions. On the one hand the states of interest have to be occupied with almost unity probability and the eigenstates of the system have to be separated in energy. In this case we can deform the confining potential using a magnetic field gradient and spill to the desired atom number (see Serwane et al., Science 332, 336 (2011)). In this way we achieve fidelities of 97% ± 2%, 93% ± 3% and 76% ± 2% for two, six and twelve particles.
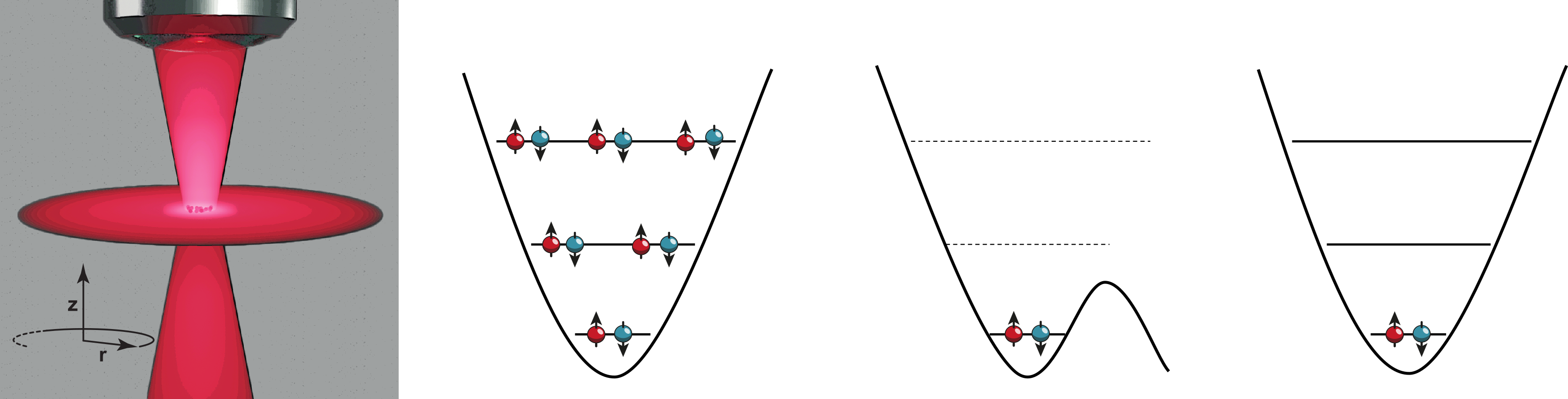
Imaging few fermion systems
We image our atoms in free space. Using a T/4 method in a harmonic trapping potential we have access to the insitu momentum distribution. The combination of our highspeed camera and high NA objective enables us to resolve individual atoms and their spin state in a single shot (see Bergschneider et al., Phys. Rev. A 97, 063613 2018).
Quenching interactions
Using a two photon Raman transition we can perform a π pulse lasting 300ns to switch between a strongly interacting and a non-interacting state. We use this technique for our imaging protocol (see Holten et al., Nature 606, 2022) and for realizing well defined interaction times during the expansion in our 2D trap. This was needed to explore hydrodynamic behaviour of our atomic gas.

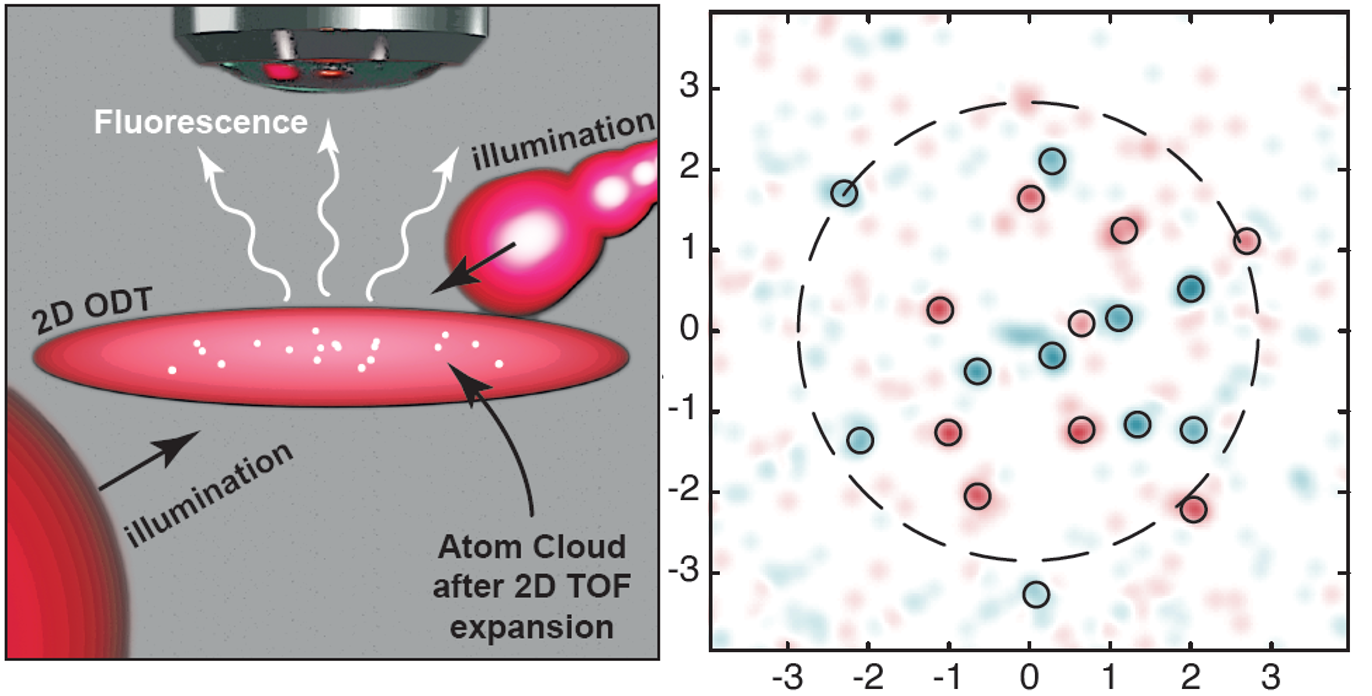
Rotating traps
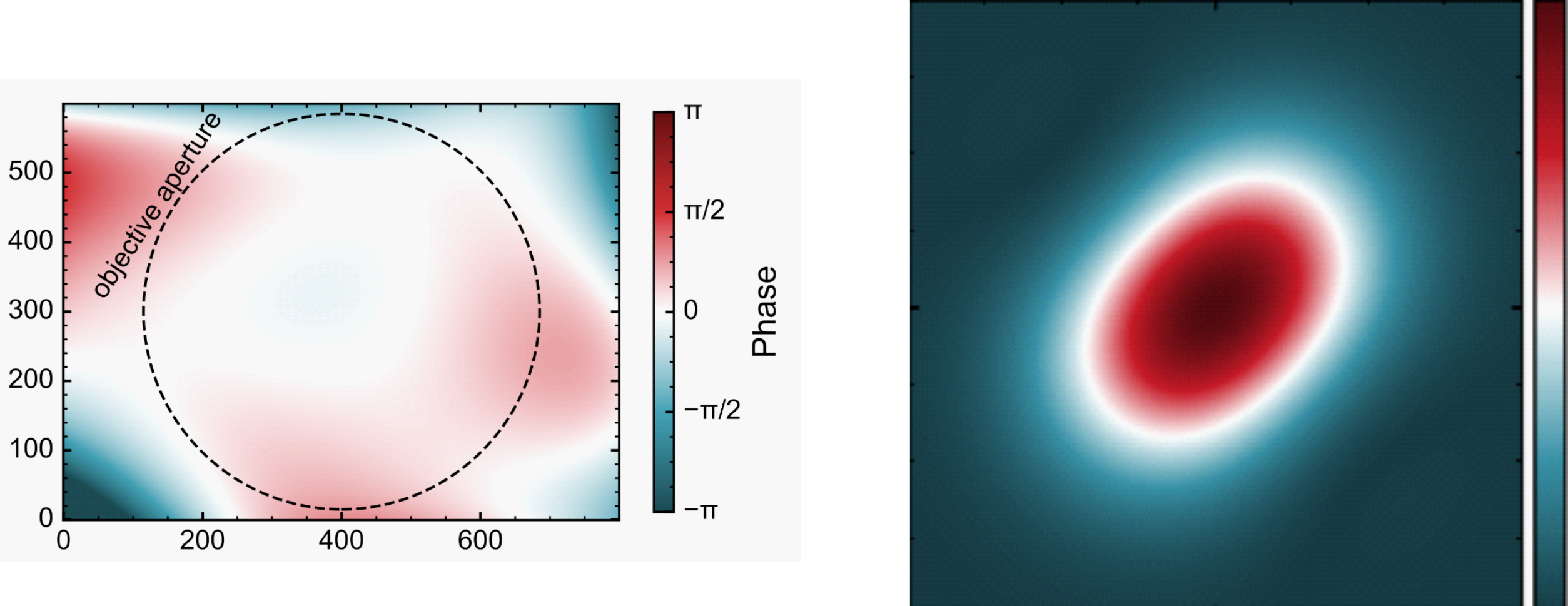
Using Spatial light modulators (SLMs) one can control the phase of a lightbeam. We put our SLMs in the optical Fourier plane such that we can do amplitude and phase modulation. In this way we create optical tweezers of differnt sizes, correct for aberrations and optical imperfections. Currently we implemented a SLM to create rotating traps. Gaussian and and higher-order Laguerre Gaussian modes are interfered. By detuning the beams with respect to each other, it is possible to create dynamic/moving traps (see L Palm et al, 2020, New J. Phys. 22 083037).
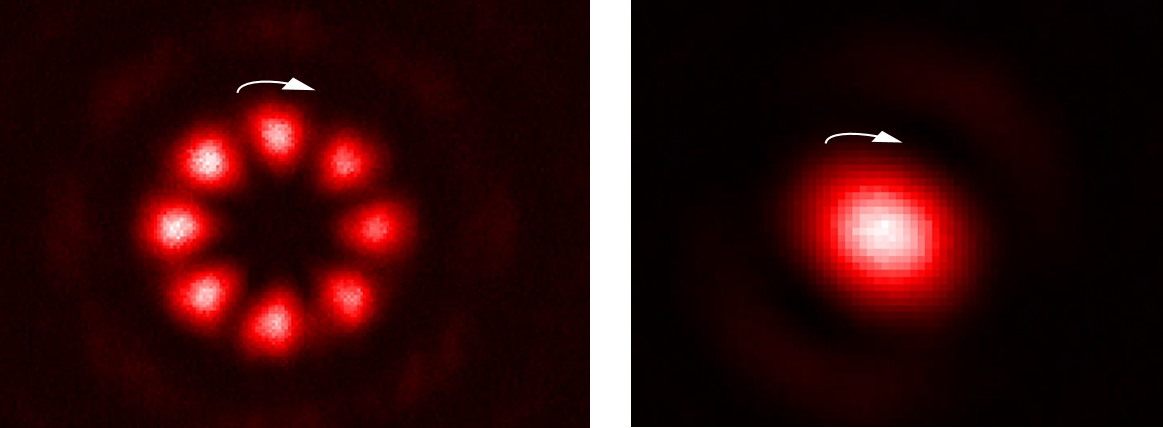
Matterwave optics
We combine matterwave optics with our capability to resolve single atoms to magnify the wavefunction of our system. A free expansion of a quantum state in a harmonic trap of trap frequency w for a quarter period of time, corresponds to a fourier transform of its wavefunction. The analogon in optics is the optical fourier transform with a lens at the focal point f. Two lenses build a telescope with magnification f1/f2. Similarly, we combine two traps of different trap frequencies w1 and w2 and magnify the wavefunction by a factor of w1/w2. This technique gives us access to the in situ positions or momenta of every single atom.
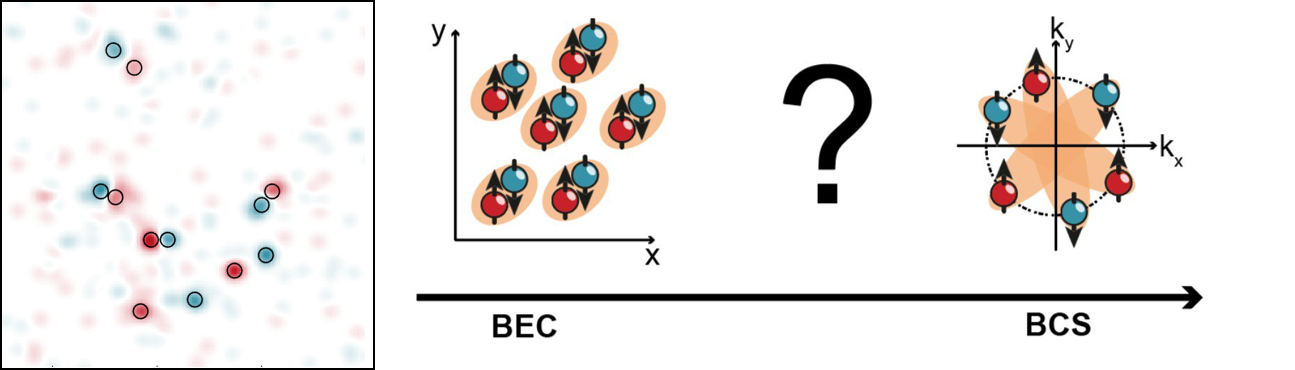
Heidelberg Quantum Architecture
The HQA experiment is the third and most recently built experiment in this group. The design process of this next generation lithium machine started in spring 2020 and is under construction since summer 2021. The experiment consists of an ultra-compact vacuum assembly including a small glass cell as a science chamber. Around the science cell a modular interface optical breadboard is located enabling interchangeability of full optical setups with accuracies better than 10µm. The last milestone was the realization of a 3D-MOT loaded by a 2D-MOT as atomic beam source.
Currently, we are setting up crucial parts of the experiment including an imaging setup with single atom sensitivity and a tweezer setup. Other ongoing projects are the implementation of magnetic field antennas for RF and micro waves and the miniaturization of an optical accordion on one of the interchangeable breadboards.
With this experiment we do a step towards programmable quantum simulation. This includes fast cycle rates of up to 10Hz and improved control and stability of the trapped atoms. First experiments could include the realization of local measurements in a complex many-body system and using these for quantum state steering.
2D Few Fermion Experiment
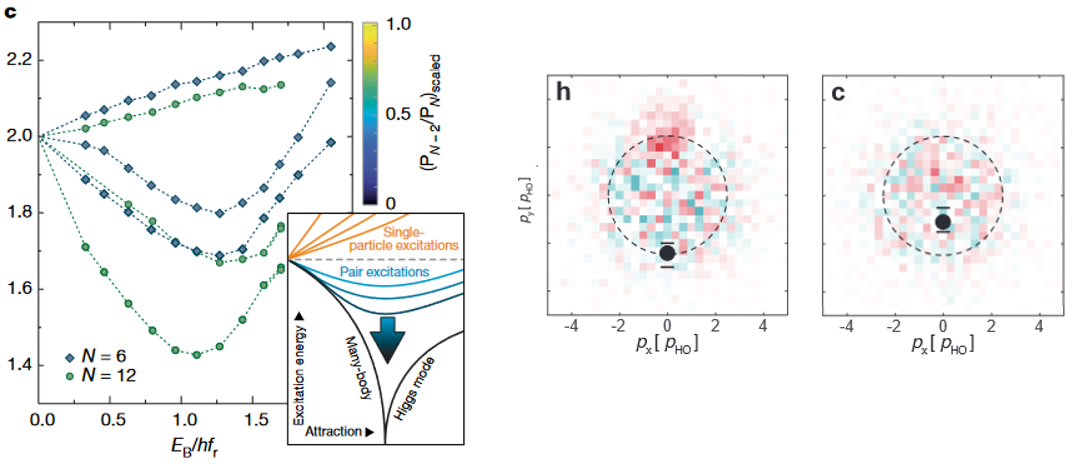
This experiment works with deterministically prepared 2D systems. Two interfering lightbeams create serveral 2D lightsheets where we can load atoms in. From the top we use a SLM to shine in a shallow beam through a high NA objective. This way we create a quasi two dimensional optical trap with a size of a few microns. In mesoscopic systems the phase diagram of the quasi-2D BEC-BCS crossover could be mapped out (see e.g. Ries et al, Phys. Rev. Lett. 114 (2015)), many-body pairing at temperatures far above the critical temperature for superfluidity was observed (see e.g. Murthy et al, Science 359, 2018) and we investigated the breaking of scale invariance in 2D Fermi gases (see e.g. Holten et al, Phys. Rev. Lett. 121, 2018). We started to investigate few body interacting quantum states. In a system of 12 atoms, we observed the precursor of the many body Higgs mode (Bayha et al., Nature volume 587, 2020) and we observed Cooper pairing (Holten et al., Nature 606, 2022).
Rotating Few Fermion Experiment
In the past, we have implemented an optical setup which allows us to rotate few Fermion systems trapped in optical potentials. This is realized by interference of a Gaussian and Laguerre-Gaussian mode generated by a spatial light modulator. The generation of these potentials requires ultra precise control. Therefore, we have implemented an algorithm which measures the optical aberrations of the system directly on the atoms.

Former Projects
Efimov physics:
We investigated universal few-body physics with three-component Fermi gases of lithium-6 atoms. We observed universal Efimov resonances both for the three-atoms and for the atom-dimer regime (see Ottenstein et al. PRL 101, 203202 (2008), Wenz et al. PRA 80, 40702 (2009), Lompe et al. PRL 105, 103201 (2010)). Furthermore, we were able to associate Efimov trimers using radio-frequency pulses and hence we could determine their binding energy as a function of the interaction strength (see Lompe et al. Science 330, 940 (2010)).
High-resolution radio frequency spectroscopy:
Making use of the small sample sizes in our few fermion setup, we could significantly improve the measurement accuracy of the lithium dimer binding energy close to the broad Feshbach resonance at about 830 Gauss. In collaboration with theorists, this allowed us to determine the lithium-6 scattering length as a function of the magnetic field with significantly improved accuracy (see Zürn et al. PRL 110, 135301 (2013)).